线性代数MIT笔记

网易公开课课程地址

方程组的几何解释

首先讲解的是"求解线性方程组"，在此列举了含有n个方程，n个未知数的这样一个方程组。我们先以二维为例：
$\left\{ \begin{array}{c} 2x-y=0 \\ -x+2y=3 \\ \end{array} \right.$，写成矩阵的形式为$\left[ \begin{matrix}2 & -1\\-1 & 2 \end{matrix} \right]$$\left[\begin{matrix}x \\ y \end{matrix} \right]$=$\left[\begin{matrix} 0 \\ 3 \end{matrix} \right]$,可以用$AX=b$来表示。
A:系数矩阵
X:未知向量
b:方程组的解

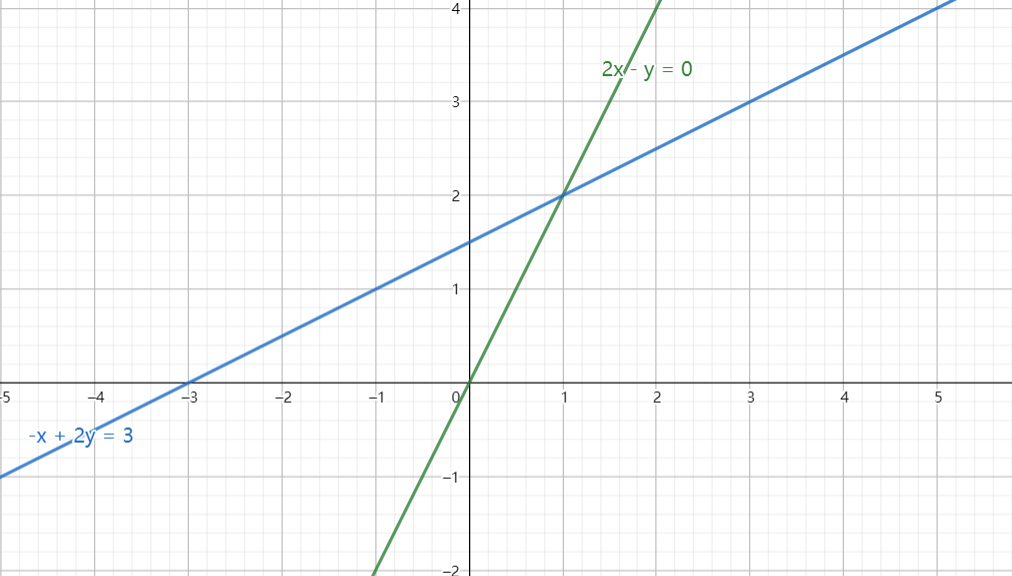
我们以首先以行的形式，做出行图像：

可以看到它们交于(1,2)点，即(1,2)点为方程组的解。
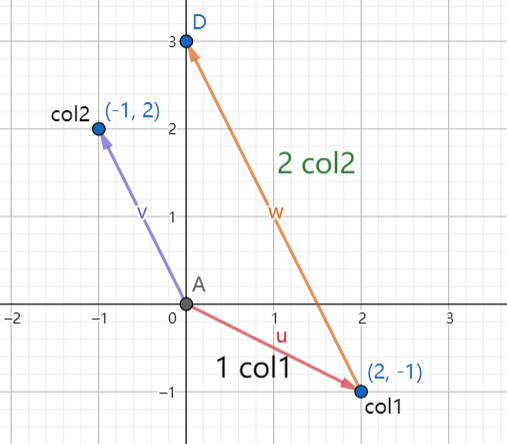
紧接着我们再做出它的列图像，即以向量的形式来做。可以这样来写$x\left[ \begin{matrix} 2 \\ -1 \end{matrix} \right]$+$y\left[ \begin{matrix} -1\\ 2 \end{matrix} \right]$=$\left[\begin{matrix} 0 \\ 3 \end{matrix} \right]$，此方程的目的是如何将左边的两个向量进行正确的线性组合，得到右边的向量,我们代入上面我们已知的解x=1,y=2。其图像为：

可以看出，最终的向量是等式右边的解。
这里有一个小疑问:所有的线性组合是什么?即选取所有的x和y，则右侧会发生什么?答案则是，我们会得到任意的右侧向量。
下面以三维为例：
$\left\{ \begin{array}{c} 2x-y=0 \\ -x+2y-z=-1 \\ -3y+4z=4 \end{array} \right.$,$A=\left[\begin{matrix} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -3 & 4 \end{matrix} \right]$,$X=\left[\begin{matrix} x \\ y \\ z \end{matrix} \right]$,$b=\left[\begin{matrix} 0 \\ -1 \\ 4 \end{matrix} \right]$
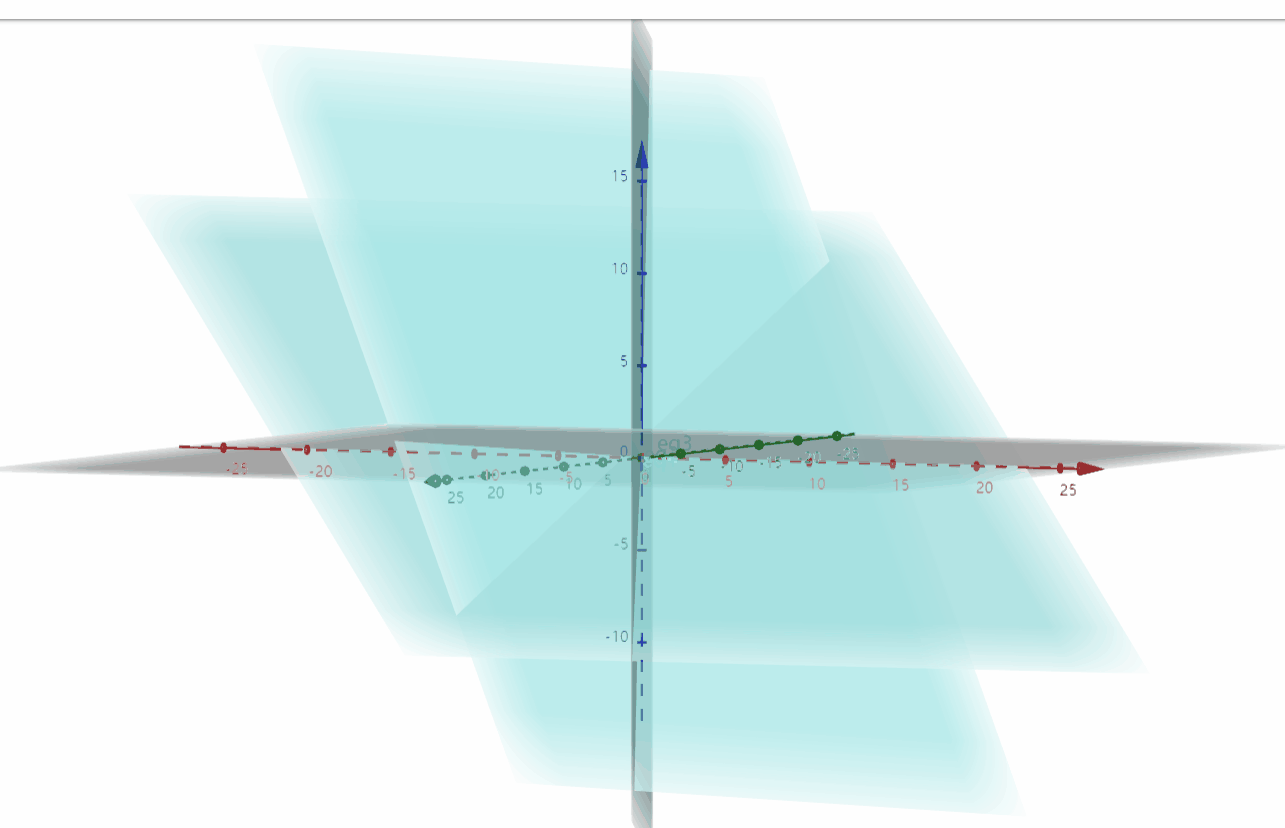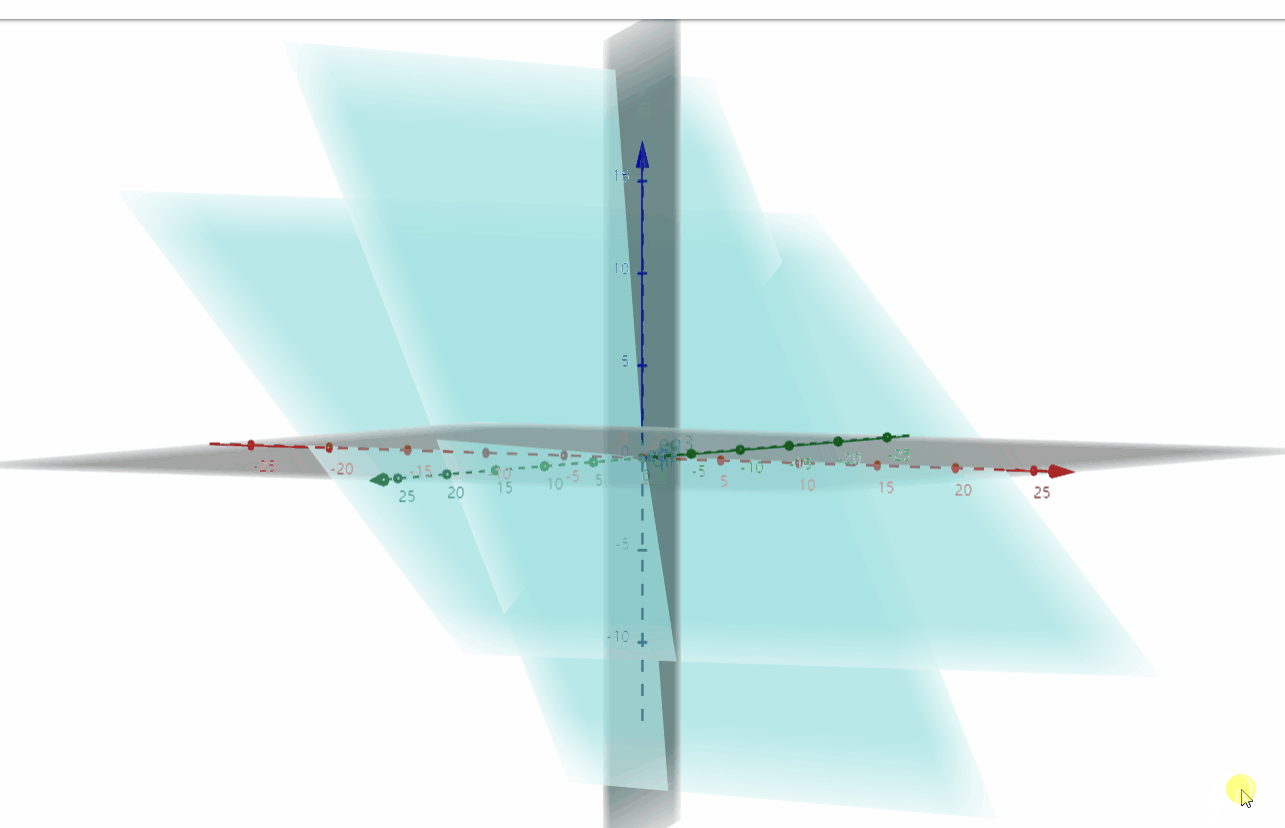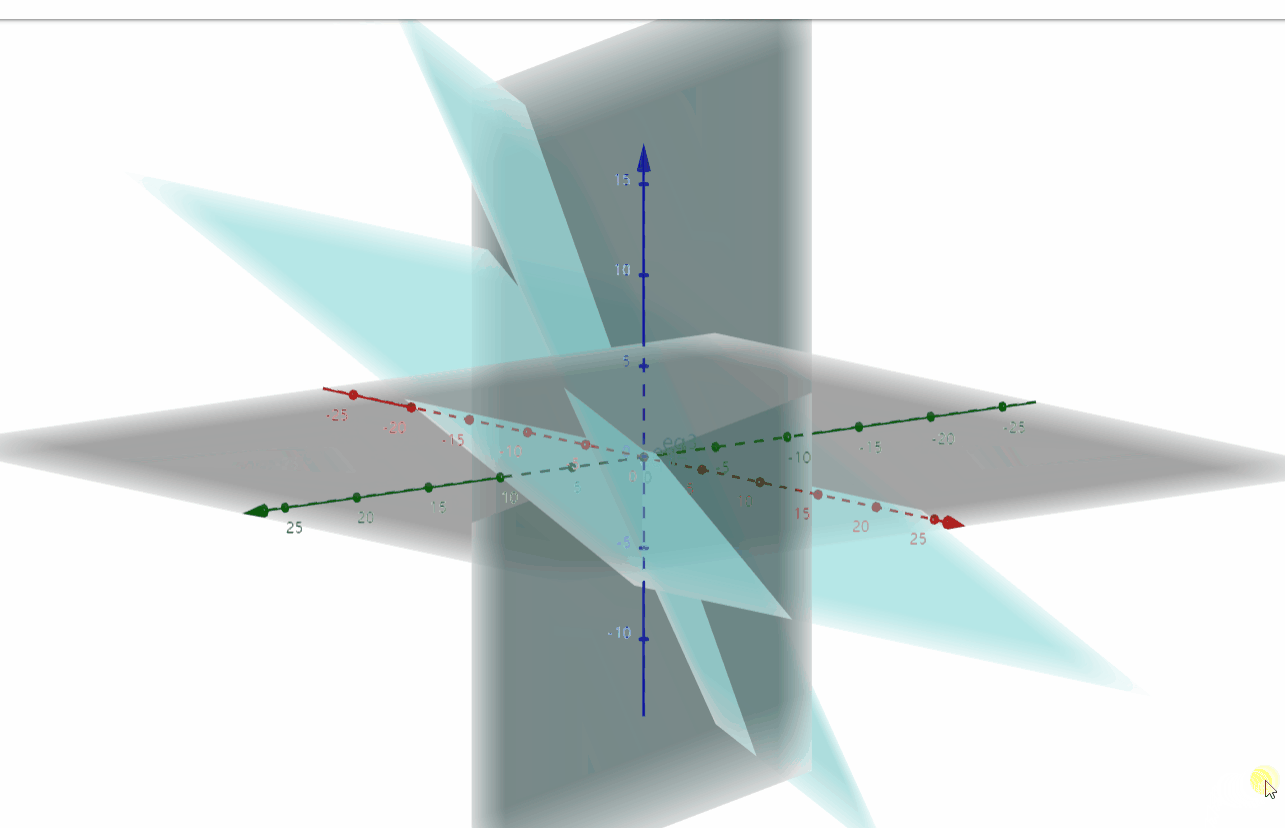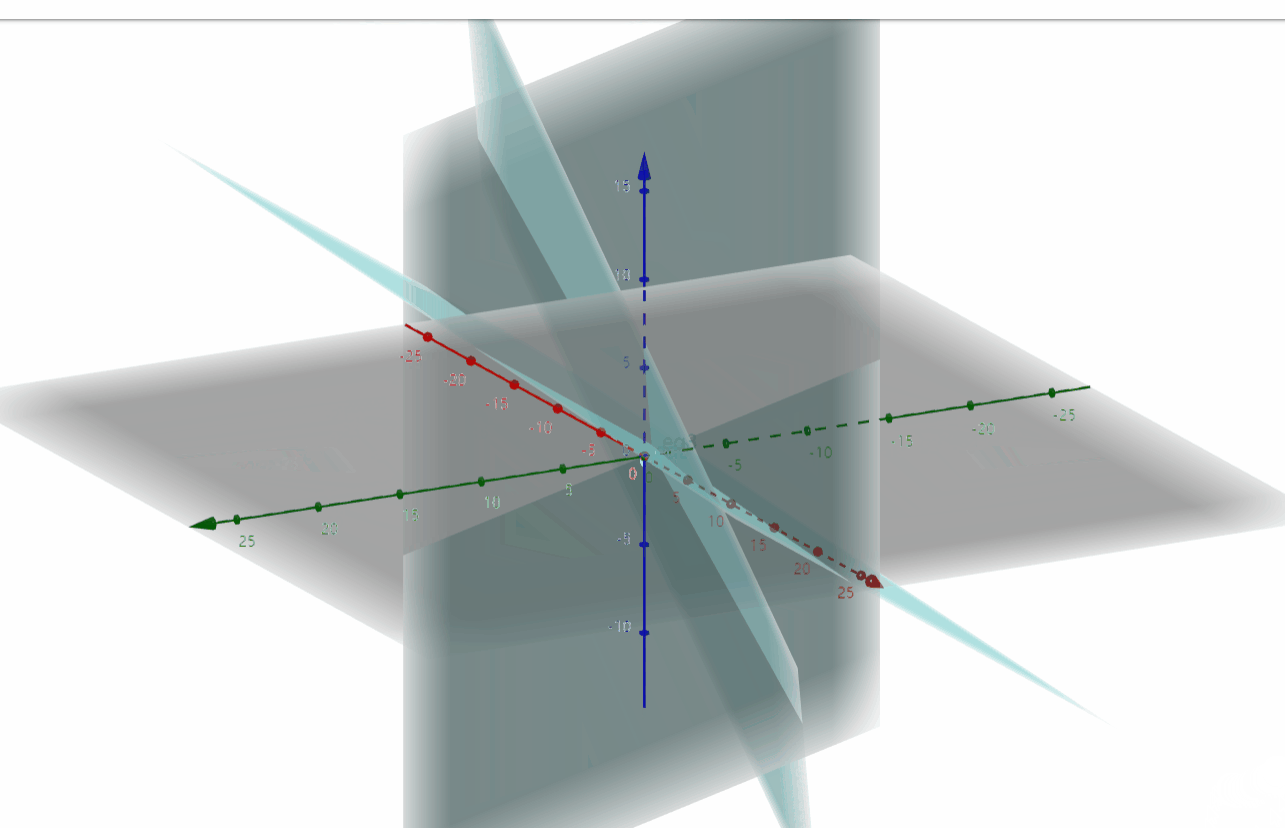
我们画出它的行图像，由此可知，三个平面的交点即为方程组的解。

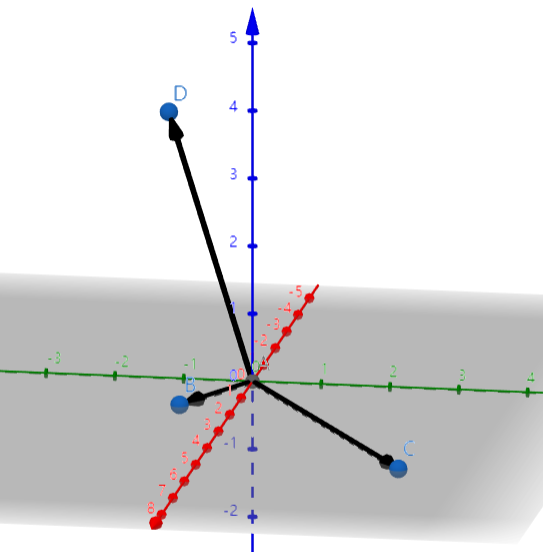
下面我们画出列图像，首先将方程写成向量的形式：$x\left[ \begin{matrix} 2 \\ -1 \\ 0\end{matrix} \right]$+$y\left[ \begin{matrix} -1\\ 2 \\ -3\end{matrix} \right]$+$z\left[ \begin{matrix} 0 \\ -1 \\ 4 \end{matrix} \right]$=$\left[\begin{matrix} 0 \\ -1 \\ 4 \end{matrix} \right]$

很显然，这是一个特殊的例题，可以看出解为x = 0,y = 0,z= 1,即第三列向量为右侧的向量，如果我们将右边的向量换为$\left[\begin{matrix} 1 \\ 1 \\ -3 \end{matrix} \right]$,我们可以看出x = 1，y = 1, z = 0。
此时有一个问题，是不是所有的b都会有对应的线性组合呢，即不论b取多少，都可以通过左边的组合来得到b。这个需要看我们的列向量，对于此例，答案是肯定的。但如果我们碰到一个新的方程组，如果是三维，它其中的两或三个向量在同一个平面上，则必然无法得到三维空间所有的b。
矩阵乘法：
对于$AX=b$，矩阵和向量如何相乘？
如：$\left[\begin{matrix} 2 & 5\\ 1 & 3 \end{matrix} \right]$ $\left[\begin{matrix} 1 \\ 2 \end{matrix} \right]$
第一种方法为：$\left[\begin{matrix} 2 & 5\\ 1 & 3 \end{matrix} \right]$ $\left[\begin{matrix} 1 \\ 2 \end{matrix} \right]$=$1\left[\begin{matrix} 2 \\ 1\end{matrix} \right]$ +$2\left[\begin{matrix} 5 \\ 3 \end{matrix} \right]$= $\left[\begin{matrix} 12 \\ 7\end{matrix} \right]$
第二种方法为点乘法，即用行来点乘向量。$2*1+5*2=12,1*1+3*2=7$.